BrainVoyager QX v2.8
EEG/MEG Source Time Course Reconstruction
In order to reconstruct the entire EEG/MEG source time-courses sÂ(t), a linear inverse operator W estimated during the EEG/MEG inverse modeling stage is applied to the measured signals m(t) at each time point t:
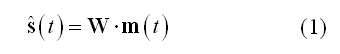
Assuming a measurement configuration with M channels, N sources and a free orientation model (i.e. X, Y and Z components are considered for each dipole), matrix W has order 3*NxM. If the orientation of each source is constrained (constrained orientation model), the order will be NxM. In practice, one or three "point" source time-series at each node i of a grid or at each vertex of the mesh (also called virtual channel) will be generated during reconstruction:
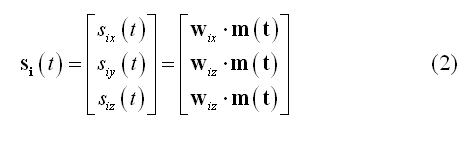
Source reconstruction at each virtual channel can be either performed on average data set (i.e. ERP/ERF data) or on each single trial of a data set. Normally, single-trial estimation is necessary for projecting narrow-band data sets representing oscillatory activity around a certain frequency, i.e. EEG/MEG time-courses that have been previously filtered according to a specific time-frequency characteristic. When (2) is applied to average data sets, m(t) is a expected to be a real-valued function and so are each component of s(t). For source localization in free orientation modeling, it is often convenient to calculate the instantaneous root-mean-square (RMS) power time-course or the decibel power time-course (DBPOW), which gives a scalar signal at each virtual channel:
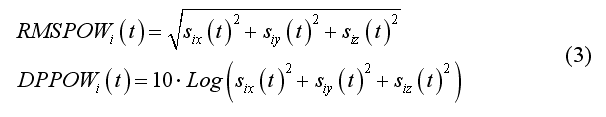
When (2) is applied to single-trial data set, m(t) is expected to be a complex-valued function, e.g. resulting from a complex (linear) signal transform (e.g. continuous wavelet transform, CWT) according to a given time-frequency characteristic. In this case, the instantaneous single-trial source time-course is complex and the single-trial source power vectorial and scalar time-courses can be computed as follows for source location i:
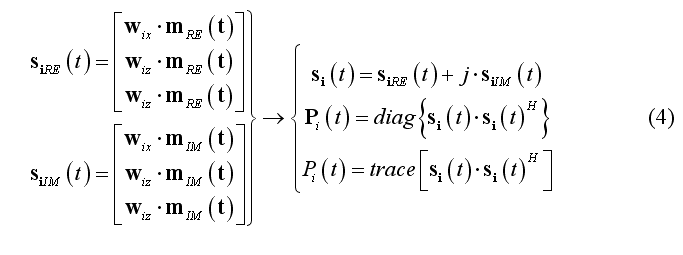
Reconstructing the source power activity at each single-trial is important in distributed source imaging and analysis for quantifying the average oscillatory power in a given time interval with respect to a trigger at each source point (see source analysis step). Combining all single-trial source power time-courses across all trials allows reconstructing in each virtual channel the so-called event-related spectral perturbation (ERSP), a useful measure for induced oscillatory activity and the often called inter-trial phase coherence (ITLC) or phase-locking value (PLV), a useful measure for describing the consistent phase locking across trials between the (complex) source signal and a "reference" signal. The reference signal can be specified as a simple sinusoidal oscillation with the same time-frequency characteristics as the source signal and with constant phase across trials or can be specified as the complex source signal from another source (source coherence), thereby providing a normalized measure for the amount of oscillatory coupling between two regions. For any virtual channel and K single trial repetitions, these two scalar time-courses can be computed as follows:
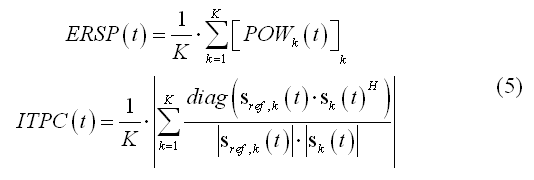
Application
In BrainVoyager QX, it is possible to reconstruct the EEG/MEG source time-course at each virtual channel (node or vertex) from the 5th tab of the EMEG Suite dialog. First of all the input data type should be selected, which will be an ACT file for trial-averaged data sets or an STD file for single-trial data sets. The result of this stage will be a new mesh time-course (MTC) defined on the current mesh in which the vertex time-course will contain the RMS power time-course evolution. Using the STD is the choice for projecting narrow-band complex signal.
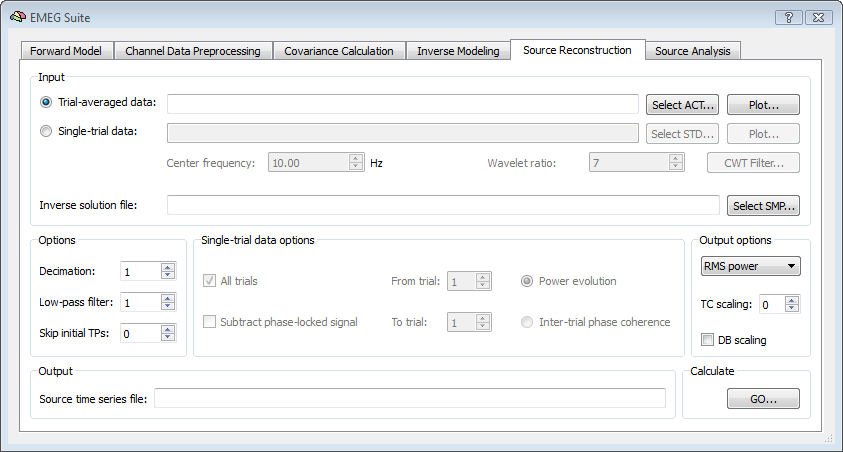
Besides the channel data set, the SMP with a pre-computed inverse solution should be selected as well. This SMP must fit the current SRF and the current settings for the orientation model (free or constrained). Other options pertain to the possibility to decimate and low-pass filter the input time-series before projection to the source space and, for single-trial data sets, the possibility to use all or part of the trials.For the output, the default settings are to generate RMS power time-courses from averaged data sets and power evolution for from single-trial data sets. Alternatively, the inter-trial phase coherence time-course can be generated from single-trial data sets and specific dipole orientation (X, Y, Z) signals from average data sets. When generating RMS power time-course it is also possible to switch from the RMS power to DB power by checking the DB scaling box. A factor for amplitude/power scaling of the time courses (scaling factor S = 0 means 10^S = 10^0 = 1) can be set. After calculations, the new MTC file will be shown as the output.
Each MTC created at this stage is also linked to a default identity sphere-to-sphere mapping (SSM) file and a default protocol (PRT) file. The SSM file is needed when one wants to combine multiple MTCs in one distributed source analysis using a GLM approach but also in the source analysis stage. The default "identity" SSM file written for the current SRF takes the name of the current mesh with the extension changed from SRF to SSM. The PRT file will only contain one default condition (called "trigger"), but can be manually edited in a later stage for specifying any intervals of activity which might of interest for a possible single- or multi-study general linear model (SS-GLM, MS-GLM) analysis, similar to what one could do with MTC consisting of fMRI time-courses.
References
Baillet, S., Mosher, J. C., Leahy, R. M., 2001.Electromagnetic Brain Mapping. IEEE Signal Processing Magazine 18, 14-30.
Brookes, M. J., Gibson, A. M., Hall, S. D., Furlong, P. L., Barnes, G. R. , Hillebrand, A., Singh K. D., Holliday, I. E., Francis, S. T., Morris, P. G., 2005. GLM-beamformer method demonstrates stationary field, alpha ERD and gamma ERS co-localisation with fMRI BOLD response in visual cortex. Neuroimage. 26, 302-308.
Brookes, M. J., Mullinger, K. J., Stevenson, C. M., Morris, P. G., Bowtell, R. 2008.Simultaneous EEG source localisation and artifact rejection during concurrent fMRI by means of spatial filtering. Neuroimage. 40, 1090-1104.
Dale, A. M., Sereno, M. I., 1993. Improved localization of cortical activity by combining EEG and MEG with MRI cortical surface reconstruction: a linear approach. J. Cogn. Neurosci. 5, 162-176.
Dale, A. M., Liu, A. K., Fischl, B. R., Buckner, R. L., Belliveau, J. W., Lewine, J. D., Halgren, E., 2000. Dynamic statistical parametric mapping: combining fMRI and MEG for high resolution imaging of cortical activity. Neuron 26, 55-67.
Darvas, F., Pantazis, D., Kucukaltun-Yildirim, E., Leahy, R.M., 2004.Mapping human brain function with MEG and EEG: methods and validation.NeuroImage 23, S289-S299.
Jeffs, B., Leahy, R., Singh, M., 1987.An evaluation of methods for neuromagnetic image reconstruction.IEEE Trans. Biomed. Eng. 34, 713-723.
Lin, F. H. , Witzel T., Hamalainen M. S., Dale A. M., Belliveau J. W., Stufflebeam S. M., 2004. Spectral spatiotemporal imaging of cortical oscillations and interactions in the human brain. Neuroimage. 23, 582-595.
Lin, F. H., Belliveau J. W., Dale A. M., Hamalainen M. S., 2006a. Distributed current estimates using cortical orientation constraints. Hum Brain Mapp. 27:1-13.
Lin, F. H., Witzel T., Ahlfors S. P., Stufflebeam S. M., Belliveau J. W., Hamalainen M. S., 2006b. Assessing and improving the spatial accuracy in MEG source localization by depth-weighted minimum-norm estimates. Neuroimage. 31, 160-171.
Liu A. K., Belliveau J. W., Dale A. M., 1998. Spatiotemporal imaging of human brain activity using functional MRI constrained magnetoencephalography data: Monte Carlo Simulations. Proc Natl Acad Sci U S A. 95, 8945-8950.
Copyright © 2014 Fabrizio Esposito and Rainer Goebel. All rights reserved.