BrainVoyager QX v2.8
EEG/MEG Channel Data Covariance Calculation
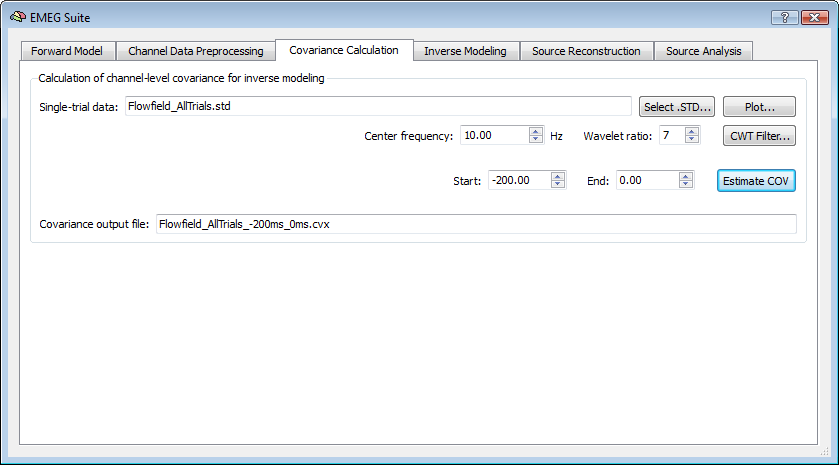
When estimating a distributed inverse solution, a data covariance matrix is often needed and can be estimated from a prepared STD file. The covariance matrix is an MxM matrix (M being the number of channels of the current configuration) that summarizes the spatial distribution in the channel space of the signal and noise power (diagonal entries) and the spatial correlations between all EEG/MEG channel recordings (off-diagonal entries). In the context of Minimum-norm techniques the covariance of the channel recordings during a "baseline" period is typically assumed as the "noise covariance" or the "baseline covariance" and represents the regularization term of the solution. The baseline covariance estimation normally entails with extracting and concatenating all pre-trigger trial interval data or by considering a separate data set with a continous pre-experimental recording period. In the context of Beamforming techniques the covariance matrix is used to quantify the amount of interference between all possible sources "visible" in the channel space and is normally calculated over a specific time or time-frequency window of interest. The bandwidth of single-trial data (STD) sets can be narrowed around a specific frequency of interest via the application of a continous wavelet transform (CWT) filter.
The third tab of the EMEG Suite allows calculating the covariance matrix of a the single-trial data (STD) set. The resulting values corresponding to all matrix entries are stored in a covariance file (CVX). Optionally a CWT filter can be applied to the STD data within the same Covariance tab. ariance tab. The options in this tab provide a way to define the intervals of data to be extracted at each epoch of the data set. Normally the pre-trigger interval of the trial is used for extracting data.
Copyright © 2014 Fabrizio Esposito and Rainer Goebel. All rights reserved.