The ‘C’ in ANCOVA
The ANCOVA module has been substantially improved in BrainVoyager QX 1.9.9 supporting many ANOVA models. Despite its name, the ANCOVA module did, however, not support true analysis of covariance models combining analysis of variance with techniques from regression analysis. With respect to the design, ANCOVA models explain the dependent variable by combining categorical (qualitative) independent variables with continuous (quantitative) variables. While there are special extensions to ANOVA calculations to estimate parameters for both categorical and continuous variables, ANCOVA models can also be calculated using multiple regression with an appropriately constructed design matrix. In the latter framework, ANCOVA is a nice example of the power of the General Linear Model (GLM) framework.
The basic idea of ANCOVA is to reduce pre-existing variability between subjects by removing the effects of continuous variables, which covary with the dependent variable. The continuous variables augment the standard ANOVA model and are called “covariates” or “concomitant variables”. If a covariate is indeed linearly related to the dependent variable, the variance of the error term in the model will be reduced by reducing inter-subject variability, which increases the sensitivity of ANOVA tests (i.e. smaller mean differences will become significant as compared to a standard ANOVA). Note that ANCOVA has a similar goal as repeated measures ANOVA in removing pre-existing differences between subjects. In repeated measures ANOVAs this is achieved by measuring the same subjects under various conditions. By analyzing only changes in the dependent variable across conditions, repeated measures ANOVA completely removes between-subjects variability. ANCOVA models are, thus, only useful for designs with between-subjects factors but provide no benefit in pure within-subjects factorial designs.
What would be good examples of ANCOVA in the context of neuroimaging data? A useful application of ANCOVA would be cortical thickness analysis. If differences in cortical thickness are investigated in several groups (e.g. one or more patient groups and a group of healthy controls), it might be very useful to eliminate the effect of age from the thickness measurements. By removing the effect of age, ANCOVA would allow to study group effects of cortical thickness measures as if all subjects would have the same age (same starting condition). In order to remove the effect of a covariate, a score (e.g. age value) has to be provided for each subject.
ANCOVA models may also be useful when comparing group effects in fMRI experiments. Since standard fMRI measurements do not provide quantitative results, this application scenario is, however, more problematic. Arterial Spin Labeling (ASL) techniques provide more quantitative functional results and should be considered if group comparisons (ANOVA/ANCOVA) are intended.
Due to across-scan variability of normal (EPI) fMRI data, condition effects (beta values) estimated per subject at the first level of random effects analysis may not be an appropriate starting point for calculating correlations with a covariate, such as age. Contrast t values might be more useful than beta values, since t values reflect condition effects normalized to the within-subject (within-voxel) measurement variability. The updated User’s Guide describes how to prepare separate-subjects GLM results for single factor ANCOVA analysis.
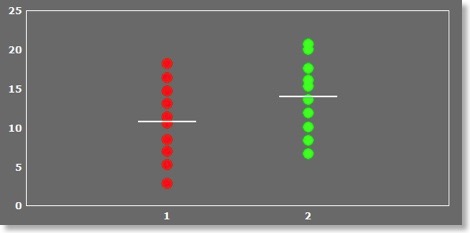
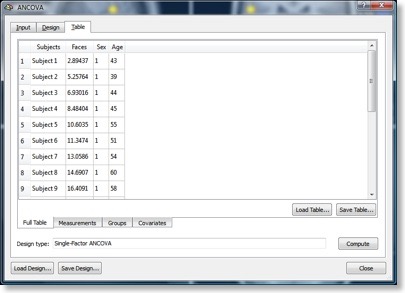
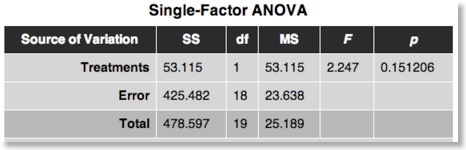
The upcoming maintenance release 1.9.10 provides support for ANCOVA models. The ANCOVA module now allows to add covariates to standard one-way (single factor) ANOVA and to two-factorial ANOVAs with one between-subjects and one within-subjects factor. In previous versions, covariates could be correlated with a dependent variable but could not be added to a ANOVA design to reduce the error variance (creation of covariate x dependent variable correlation maps is, unfortunately, broken in 1.9.9 but has been fixed in 1.9.10). I will briefly describe the single factor ANCOVA with simulated data; for a detailed description, check the updated User’s Guide, which will be available at the time of the 1.9.10 release. Using the GroupDataSimulator, data was created for 20 subjects for two groups of 10 subjects each. The GroupDataSimulator has been updated (version 1.5) in order to allow modeling subject-specific condition effects. This feature was used to simulate linearly increasing values for the subjects in each group. Furthermore, the means of the two groups differed from each other. The difference is relatively small as compared to the variability within the two groups. The figure above shows in red the values of group 1 (“male”) and in green the values of group 2 (“female”) extracted from a simulated volume-of-interest (VOI). If this data is submitted to a single factor ANOVA, the following results are obtained, showing that the difference between the two groups does not reach significance:
The ANOVA can be extended to an ANCOVA by adding a covariate (e.g. “age”) in the design. The values of the covariate can be entered in the “Age” column in the data table. In BV QX 1.9.10, sub tables have been added allowing to view separately measurement, grouping and covariate columns. Since each sub-table also comes with load and save buttons it is now possible to flexibly augment different designs by adding grouping or covariate information. The figure below shows the same data as above but now as a scatter plot using the entered “age” covariate. Each point shows, as before, the statistical fMRI value on y axis and the corresponding score of the covariate (age) at the x axis. The lines within the data of each group are regression lines showing that there is a strong linear correlation between simulated age and fMRI measurements.
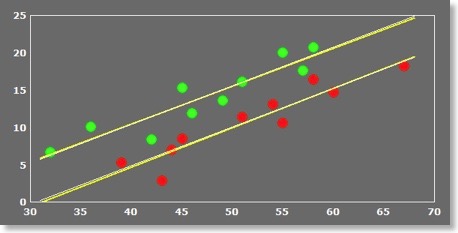
Note that the error variability is now reduced to the squared vertical distance of each point with respect to the estimated group regression line instead of to the group mean. This substantially reduces the variance of the error term and leads to highly significant statistical results as can be seen in the resulting ANCOVA table:
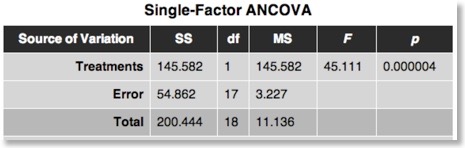
An important prerequisite of ANCOVA is that the regression lines are the same for each group, otherwise the covariate would interact with the independent categorical variable. When the slopes are not parallel, covariance analysis is not appropriate. In BV 1.9.10 this prerequisite of parallel regression lines (homogeneous slopes) is tested and shown in the ANCOVA output:
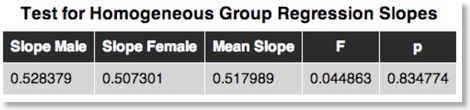
This table shows the values for the slope in each group (“Male” and “Female” in this example), the mean slope and an F value testing whether the group slopes differ significantly from the mean slope. While we normally look for significant F values, this test should show a non-significant result indicating that the slopes are parallel at the population level. If the F test is significant, the ANCOVA model should not be used for the data set.
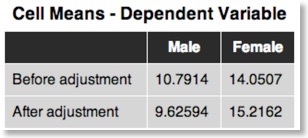
The produced ANCOVA output includes also a table (see snapshot above) showing the values of the group means. The normal mean values are shown in the “Before adjustment” row but there is an additional row showing “adjusted” means. These latter values correct for different means of the covariate in the groups: If one group (despite randomization) ends up having older people, the mean value of the dependent variable will be increased in that group as compared to the other group in case that age is (positively) correlated with the dependent variable. The adjusted means, thus, compensate for different starting values with respect to the covariate.
In summary, ANCOVA uses the relationship between the dependent variable (e.g. fMRI t values, cortical thickness measurements, DTI FA measurements) and one or more quantitative variables (covariates) for which observations are available (e.g. age, IQ) in order to reduce the error term variability leading to a more powerful study for comparing effects of the independent variable.