BrainVoyager QX 2.0 - Episode 2: MVPA Basics
April 07, 2009
One of the most important new feature of the upcoming 2.0 release of BrainVoyager QX is a set of tools for multi-voxel pattern analysis (MVPA). MVPA is gaining increasing interest in the neuroimaging community because it allows to detect differences between conditions with higher sensitivity than conventional univariate analysis by focusing on the analysis and comparison of patterns of activity. In such a multivariate approach, data from individual voxels within a region are jointly analyzed. Furthermore, MVPA is often presented in the context of “brain reading” applications reporting that specific mental states or representational content can be decoded from fMRI activity patterns after performing a “training” or “learning” phase. In this context, MVPA tools are often referred to as “classifiers” or, more generally, “learning machines”. The latter name stresses that many MVPA tools originate from a field called “machine learning”, a branch of artificial intelligence.
Basic Concepts
It might be helpful to introduce a few distinctions and application scenarios influencing the choice of multivariate analysis tools. First, “supervised” and “unsupervised” multivariate analysis (learning) methods are distinguished. Unsupervised methods (not further considered here) attempt to find structure in the data without using knowledge of the conducted tasks (e.g. ICA). Supervised methods on the other hand explicitly use knowledge of the experimental protocol.Learning, Testing and Generalization Performance
Available data is divided in two sets, a “training” and a “test” set. The training set is used during the “learning phase” to estimate a function which maps brain activation patterns (input) to corresponding class labels (target). As an example, consider a study presenting different images of object categories, such as “houses” and “faces”. All brain activation patterns in the training set evoked when subjects looked at houses would be labeled as “house class”, those patterns evoked when subjects looked at faces would be labeled as “face class” and so on. After the training phase, the learning machine should be able to correctly classify not only the learned activity patterns but also novel activation patterns (test data) as belonging to the “house” or “face” class. Note that the output on test input data with known target labels is crucial for assessing the generalization performance of a classifier. A classifier that learns correctly all input-target pairs, but performs at chance level for new data would be useless. Poor generalization performance indicates overfitting, i.e. the classifier might have learned the training exemplars “too well”. Some neural network classifiers suffer from this problem. The support vector machine (SVM) on the other hand is a “smart” classifier because it avoids overfitting the data ensuring optimal generalization performance.Voxels = Features
An exemplar (input pattern) used during learning is represented as a feature vector x with N elements. The value of an element usually specifies the presence of a certain feature. What are the “features” in fMRI activity patterns? In most applications, a feature refers to a response measure of a specific voxel. The dimension N of a fMRI feature vector, thus, corresponds to the number of included voxels in the analysis. If all (brain) voxels are included, this will lead to hundred thousand or more “features”, which will make it difficult to learn the right classification function from a few activation patterns. Such situations with many features but relatively few training exemplars are characterized as suffering from the “curse of dimensionality”.ROI Analysis or Whole-Brain Mapping?
To solve this problem, classifiers are often applied to response patterns originating from a reduced number of voxels, e.g. from voxels of anatomically or functionally defined regions-of-interest (ROIs). This typically results in feature vectors with dimensions in the order of hundreds or thousands of voxels. With 10-100 training exemplars, such problems are suited for standard classifiers, such as support vector machines (SVMs), which will be treated in more detail in the next blog.A problem with the ROI approach is that one often does not know the locations a priori where different conditions may be separated using multivariate analysis tools. In these situations, one would like to find the discriminative brain regions. In other words, one is interested in multivariate brain mapping. But how can this be done without getting lost in the curse of dimensionality? One proposed solution is the “searchlight” approach. As in univariate analysis, each voxel is visited, but instead of using only the time course of the visited voxel for analysis, several voxels in the neighborhood are included forming a set of features for joined multivariate analysis. The neighborhood is usually defined roughly as a sphere, i.e. voxels within a certain distance from the visited voxel are included. The result of the multivariate analysis is then stored at the visited voxel (e.g. a t value resulting from a multivariate statistical comparison). By visiting all voxels and analyzing their respective (partially overlapping) neighborhoods, one obtains a whole-brain map in the same way as when running univariate statistics. Since the performed multivariate analysis operates with voxels in a neighborhood, this approach is also called local pattern effects mapping.
While the searchlight mapping approach is very attractive, it makes the strong assumption that discriminative information is located within small brain regions. While this assumption is surely appropriate in light of the known functional organization of the brain, there are also situations where discriminative voxels are distributed more widely, e.g. in both hemispheres or extended across several areas along a processing stream. What one would like in such situations is to include initially voxels from a large region (up to the whole brain) and to gradually exclude non-discriminative features until a core set of voxels remains with the highest discriminative power. Such techniques have been indeed developed in machine learning and introduced to neuroimaging. We will have a closer look to one of these techniques, called recursive feature elimination (RFE), in a subsequent blog.
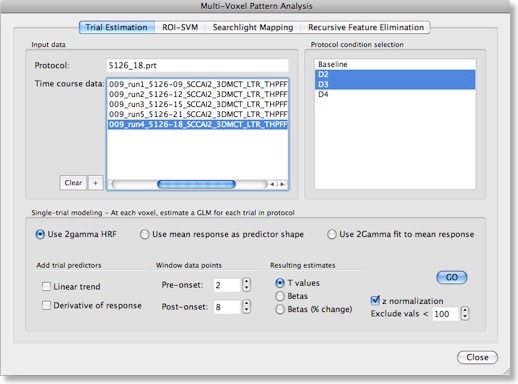
The snapshot above shows the multivariate-voxel pattern analysis (MVPA) dialog of BrainVoyager QX 2.0. The names of the tabs indicate the tools described above, including “ROI-SVM”, “Searchlight Mapping” and “Recursive Feature Elimination”. The snapshot shows the first tab of the MVPA dialog called “Trial Estimation” containing important tools to estimate activation responses at each voxel for each individual trial of each condition.
The preparation of MVPA begins with the selection of the time course data (one VTC file for each included run) of the respective experiment, which will be listed in the “Time course data” box. After selecting the data files, the involved experimental conditions are extracted from the referenced protocols and displayed in the “Protocol condition selection” box. In the example data shown in the dialog above, the conditions are “Baseline”, “D2”, “D3” and “D4” (the “D’s” represent digits of the hand in the context of a somatosensory experiment). BrainVoyager automatically selects the first two main conditions (assuming that the first condition is “baseline” or “rest”) as targets for single-trial estimation, but you can select more conditions (e.g. “D4”) in case multiple pairwise classifications are planned (e.g. “D2 vs D3”, “D2 vs D4, “D3 vs D4”).
Estimating Single-Trial Responses for Each Voxel
In order to obtain as many training exemplars as possible for each class, response values are extracted or estimated for each individual trial as opposed to estimating a voxel’s condition mean response in a standard GLM. Estimated single-trial responses across relevant voxels (e.g. from a region-of-interest) then form the feature vectors used to train the classifier. The estimated trial response might be as simple as the activity level at a certain time point (e.g. at the time of the expected hemodynamic peak response) or the mean response of a few measurement points. More often, however, a GLM is used to fit an expected hemodynamic response to the measured trial data. The beta value estimating the amplitude of the hemodynamic response is then used as the trial response value. For a more stable fit of the model, additional confound predictors (next to the constant) can be added, such as a predictor for estimating a linear trend or a predictor of the derivative of the expected hemodynamic response. Instead of estimated beta values, t values of the betas may be chosen as output. After clicking the “GO” button, the trial estimates are calculated and stored in volume map (VMP) files. For each included time course file, a corresponding VMP output file will be created.In the next episode we present a gentle introduction of support vector machines (SVMs). An understanding of the basic principles of SVMs helps to elucidate why this classifier has become so popular.